Page 78 - Capire la matematica

2
Un trinomio è scoponobile in fattori se ∆ ≥ 0, e più precisamente, se ∆ > 0: ax + bx + c =
2
2
a (x - x1) (x - x2); se ∆ = 0 ∶ ax + bx + c = a (x - x1) ; mentre quando ∆ < 0, il trinomio è
irriducibile in R.
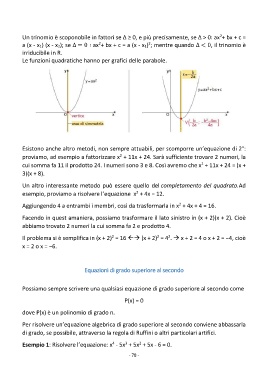
Le funzioni quadratiche hanno per grafici delle parabole.

Esistono anche altro metodi, non sempre attuabili, per scomporre un’equazione di 2°:
2
proviamo, ad esempio a fattorizzare x + 11x + 24. Sarà sufficiente trovare 2 numeri, la
2
cui somma fa 11 il prodotto 24. I numeri sono 3 e 8. Così avremo che x + 11x + 24 = (x +
3)(x + 8).

Un altro interessante metodo può essere quello del completamento del quadrato.Ad
2
esempio, proviamo a risolvere l’equazione x + 4x = 12.
2
Aggiungendo 4 a entrambi i membri, così da trasformarla in x + 4x + 4 = 16.

Facendo in quest amaniera, possiamo trasformare il lato sinistro in (x + 2)(x + 2). Cioè
abbiamo trovato 2 numeri la cui somma fa 2 e prodotto 4.

2
2
2
Il problema si è semplifica in (x + 2) = 16 → (x + 2) = 4 . → x + 2 = 4 o x + 2 = −4, cioè
x = 2 o x = −6.

Equazioni di grado superiore al secondo

Possiamo sempre scrivere una qualsiasi equazione di grado superiore al secondo come

P(x) = 0

dove P(x) è un polinomio di grado n.

Per risolvere un’equazione algebrica di grado superiore al secondo conviene abbassarla
di grado, se possibile, attraverso la regola di Ruffini o altri particolari artifici.

4
2
3
Esempio 1: Risolvere l’equazione: x - 5x + 5x + 5x - 6 = 0.
- 78 -