Page 902 - Capire la matematica
P. 902
La derivata prima è la disequazione f ′(x) ≥ 0 cioè:
è verificata per x > -1.
Pertanto la funzione è crescente per x > -1 e decrescente altrimenti.
La derivata seconda è: e la disequazione f ′′(x) ≥ 0 cioè:
è verificata per x ≤ - 2 e x≥ 0.
Pertanto la funzione è concava per x ≤ - 2 , x ≥ 0 e convessa altrimenti; inoltre presenta
un punto di flesso proprio ascendente per x = -2 e un punto di flesso proprio discendente
per x = 0: O ≡ F1(0, 0), F2(−2, 2).
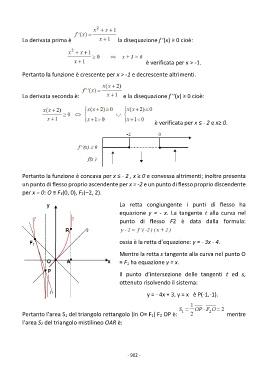
La retta congiungente i punti di flesso ha
equazione y = - x. La tangente t alla curva nel
punto di flesso F2 è data dalla formula:
ossia è la retta d’equazione: y = - 3x - 4.
Mentre la retta s tangente alla curva nel punto O
≡ F1 ha equazione y = x.
Il punto d’intersezione delle tangenti t ed s,
ottenuto risolvendo il sistema:
y = - 4x + 3, y = x è P(-1,-1).
Pertanto l’area S1 del triangolo rettangolo (in O≡ F1) F2 OP è: mentre
l’area S2 del triangolo mistilineo OAR è:
- 902 -