Page 459 - Capire la matematica
P. 459
e) f(x – α): il grafico si ottiene spostando quello di f(x) di α lungo l’asse x;
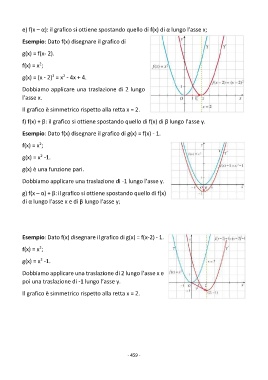
Esempio: Dato f(x) disegnare il grafico di
g(x) = f(x- 2).
2
f(x) = x ;
2
2
g(x) = (x - 2) = x - 4x + 4.
Dobbiamo applicare una traslazione di 2 lungo
l’asse x.
Il grafico è simmetrico rispetto alla retta x = 2.
f) f(x) + β: il grafico si ottiene spostando quello di f(x) di β lungo l’asse y.
Esempio: Dato f(x) disegnare il grafico di g(x) = f(x) - 1.
2
f(x) = x ;
2
g(x) = x -1.
g(x) è una funzione pari.
Dobbiamo applicare una traslazione di -1 lungo l’asse y.
g) f(x – α) + β: il grafico si ottiene spostando quello di f(x)
di α lungo l’asse x e di β lungo l’asse y;
Esempio: Dato f(x) disegnare il grafico di g(x) = f(x-2) - 1.
2
f(x) = x ;
2
g(x) = x -1.
Dobbiamo applicare una traslazione di 2 lungo l’asse x e
poi una traslazione di -1 lungo l’asse y.
Il grafico è simmetrico rispetto alla retta x = 2.
- 459 -