Page 252 - Capire la matematica

Rappresentazione grafica delle funzioni goniometriche elementari

Definizione: Dato un angolo diciamo sua misura in radianti il rapporto tra l’arco che in-

tercetta l’angolo considerato come angolo al centro di una data circonferenza e il raggio
della stessa circonferenza.

Definizione: Data una funzione y = f(x), diciamo suo dominio o insieme di esistenza, la

totalità dei valori di x per i quali esiste f(x). Diciamo suo codominio la totalità dei valori y
per i quali l’equazione y = f(x) ammette almeno una soluzione nell’incognita x.

Definizione: Data una funzione y = f(x), diciamo che essa è periodica di periodo il numero
reale P diverso da zero, se si ha:

f(x + P) = f(x), ∀ x ∈ dom(f).

1
Esempio: Data la funzione y = , il suo dominio è dato da tutti i numeri reali escluso 1,
−1
perché annulla il denominatore e la funzione non avrebbe significato. Invece il suo co-
1
dominio è dato da tutti i numeri reali escluso lo zero, poiché l’equazione y = ha come
−1
1 1
soluzione: x-1 = →x = + 1, che è un numero reale per tutti gli y tranne che per y = 0.

1
La funzione non è periodica per nessun numero reale P, perché l’equazione =
−1
1
→ x - 1 = x + P – 1 → 0 = P che ha soluzione solo per P = 0.
+−1
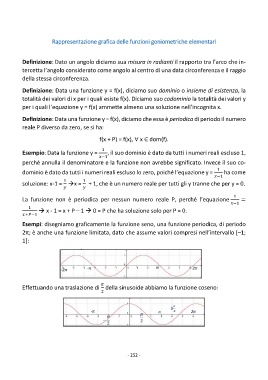
Esempi: disegniamo graficamente la funzione seno, una funzione periodica, di periodo

2π; è anche una funzione limitata, dato che assume valori compresi nell’intervallo [–1;
1]:

-2π -π π 2π

Effettuando una traslazione di della sinusoide abbiamo la funzione coseno:
2

3
-π π ∙ 2π

−

- 252 -